|
Scientific Measurement: Presentation of Data
I. Scientific Notation
The speed of light = 300,000,000 meters per second
The mass of the earth = 6,000,000,000,000,000,000,000,000 kg
The mass of an electron = 0.000000000000000000000000000091 g
The wavelength of light = 0.000059 cm
A number written in scientific notation is in the form:
____________
where n = the _______________ and 1 < ______ < 10
and m = the __________________ and m is a positive or negative
integer
To express a number in standard scientific notation:
1) ______________________________________________________
________________________________________________________
2) ______________________________________________________
________________________________________________________
3) Write the _________________ as 10 raised to the power equal to the
number from step 2.
4) If the decimal was moved to the _________, the exponent is _________;
if the decimal was moved to the ________ the exponent is ____________
and a (-) sign is inserted before the exponent.
Example 1: Express 784,000 miles in scientific notation.
7 8 4
0 0 0. miles
therefore, 105 ____________ because decimal
was moved to the ________
Answer: ________________________ miles
Example 2: Express 0.00015 meters
0. 0
0 0 1
5 meters
therefore, ______ ________________ because decimal was
moved to ______________
Answer: ___________________ meters
Example 3: Convert 428.5 x 10 9 seconds to standard
scientific notation.
First convert 428.5 to scientific notation = ______________________
Now, you have 4.285 x 10 2 x 10 9
Answer: ___________________________
Rules for exponents
1) (am) x (an) = a m+n
ex.
2) a m = a (m-n)
a n
ex.
3) (a m) n = a mn
ex.
4) n a m = a m/n
Calculations in Scientific Notation
1) When multiplying numbers in scientific notation, the coefficients are
_______________ and the exponents are ______________.
(n x 10 m) (X x 10 y) = nX x 10 (m+y)
Example: Multiply 4 x 10 2 by 5 x 10 3
Solution:
Answer =
2) When dividing numbers in scientific notation, the coefficients are
________________, and the denominator exponent is _______________ from
the numerator exponent.
n x 10 m = n x 10 (m-y)
X x 10 y X
Example: Divide 7.5 x 10 6 by 2.5 x 10 2
Solution:
3) Adding or subtracting numbers in scientific notation, when both
numbers are to the same power of 10, is done by adding or subtracting
the coeffecients and keeping the same power of 10.
Example: Add 5.0 x 105 kJ
and 4.8 x 105 kJ
Solution:
Answer:
Example: Add 2.52 x 10 4 and 2.43 x 10 3
Solution:
Then:
Answer =
Calculator Practice:
Example: 8.0 x 10
6 J
2.0 x 10 3 s
Solution (without calculator) = 8.0 x 10 (6-3)
= 4.0 x 10
3 J/s
2.0
Solution (with calculator)
Enter 8.0, then press [2nd] [EE ] 6
You see 8.0 E 6
Now press [divided by] 2.0 [2nd] [ EE] 3
Press Enter
Answer: 4000 = 4.0 x 10 3 J/s
2) Example
45 meters
(32 sec) (88 sec)
___________ Solution:
Enter 45
[Divide] by 32 x 88
Solution:
II. Significant Figures
A. Significant Figures
1. Meter Stick
Example 1:
Example 2:
Example 3:
Example 4:
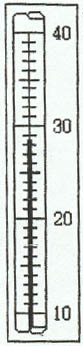
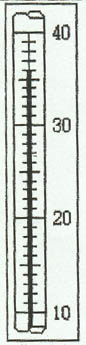
2. Thermometer
Example 1:
Example 2:
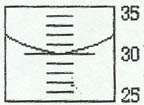
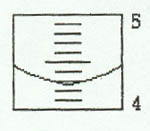
3. Graduated Cylinder
Example 1:
Example 2:
4. Electronic Balance
B. Significant Figure RULES
1. Digits other than zero are always significant.
Example: 45.85 g has _________ significant figures
2. Zeros between other digits, whether to the left or the right of the
decimal point are significant.
Example. 405.85 g has _____ significant figures
Example. 45.805 g has ______ significant figures
3. Zeros to the right of the decimal point are significant when
positioned to the right of the last nonzero digit.
Example. 16.100 g has _____ significant figures
Example. 2.500 x 103 m has ______ significant figures
Example. 2500 m has ______ significant figures
4. Zeros to the left of the first nonzero digit are not significant.
Example. 0.00078 kg has _____ significant figures
5. Zeros to the left of the decimal point on numbers less than one
are
not significant.
Example:
6. Exact numbers have an infinite number of significant figures.
Example:
Example:
C. Math with Significant Figures
1. Addition and Subtraction with Significant Figures
a) Count the number of significant figures in the decimal portion of
each number in the problem.
b) Add or subtract as indicated in the problem.
c) Round the answer so that is contains only as many decimal places as
the number in the problem that contains the LEAST number of decimal
places.
Example:
345.98 g + 78.8 g
Solution:
Number of sig figs after decimal pt:
Answer = __________ g
Example:
677.1 cm - 20.98 cm
Solution:
677.1 cm - 20.98 cm = ____________
Number of sig figs after decimal pt: _______
Answer = ___________ cm
2. Multiplication and Division with Significant Figures
The LEAST number of significant figures in any number of the problem
determines the number significant figures in the answer.
Example 1:
(1.13 m) x (5.1267 m)
Solution:
(1.13 m) x (5.1267 m) = _______ m 2
Number of sig figs:
_____ _____
Answer = _________ m 2
Example 2:
6789.7 m / 60.0 s
Solution:
6789.7 m / 60.0 s = _______ m/s
number of sig figs: ______ / ______
Answer = _________ m/s
Example 3:
2.897 x 102 m 2 / 3.4 x 10 m
2.897 x 102 m 2 / 3.4 x 10 m = _______ m
number of sig figs: _____/ _____
Answer = __________ m
REVIEW OF SIG FIGS
III. Units
A. Seven Base Units
Physical Quantity
Name of SI unit
Symbol for SI unit
length
meter
m
mass
kilogram
kg
time
second
s
electric
current
ampere
A
temperature
Kelvin
K
amount of
substance
mole
mol
luminous
intensity
candela
cd
1 meter is the distance light travels in a vacuum in 1/299,792,458
second.
1 kg is a platinum-iridium cylinder.
1 second is 9,192,631,770 oscillations of cesium atoms
absorbing microwave radiation.
Non SI units used often in Chemistry:
1) Liter = L
measure of volume
2) Cubic centimeters = cm3
measure of volume (1 mL = 1 cm3)
3) Angstrom = A
measure of length (1 A = 10-8 cm)
B. Metric Prefixes
Prefix Symbol Numerical
Multiplier
Exponential Factor
yotta Y
1,000,000,000,000,000,000,000,000
10 24
zetta Z
1,000,000,000,000,000,000,000
10 21
exa E
1,000,000,000,000,000,000
10 18
peta P
1,000,000,000,000,000
10 15
tera T
1,000,000,000,000
10 12
giga G
1,000,000,000
10 9 *
mega M
1,000,000
10 6 *
kilo k
1,000
10 3 *
hecto h
100
10 2
deca da
10
10 1
no prefix means: 1
10 0 *
deci d
0.1
10 -1 *
centi c
0.01
10 -2 *
milli m
0.001
10 -3 *
micro
0.000001
10 -6 *
nano n
0.000000001
10 -9 *
pico p
0.000000000001
10 -12 *
femto f
0.000000000000001
10 -15 *
atto a
0.000000000000000001
10 -18
zepto z
0.000000000000000000001
10 -21
C. Units Derived From Base Units
1. Area
length x length
units: m 2, cm 2, etc.
2. Volume (the amount of space an object takes up)
length x length x length
units: m 3, cm 3, or mL,
L, etc. (SI unit is ______)
Vrectangular solid = L x W x H
Vcylinder = D 2 H
4
3. Pressure (force exerted per unit of surface area)
units: N/m 2,
Pa (pascal), atm, mm Hg, etc.
Note: Extensive vs. Intensive Properties
_______________________________ - depends on the amount
of substance present
_______________________________ - independent of the
amount of substance
4. Energy (the capacity to do work)
(kg x m 2 ) / s 2
units: J (joule), calorie
5. Density
symbol =
____________________ property
definition:
equation:
Examples:
1) A block of aluminum occupies a volume of 15.0 mL and has a mass
of 40.5 g. What is the density?
2) Mercury metal is poured into a graduated cylinder that holds
exactly 22.5 mL. The mercury used to fill the cylinder has a mass
of 306.0 g. From this information, calculate the density of
mercury.
3) Find the mass of 250.0 mL of benzene. The density of
benzene is 0.8765 g/mL.
4) What volume of silver metal has a mass of exactly 2500.0 g?
The density of silver is 10.5 g/cm3.
Challenge Density Problems:
1) Lithium is a soft, gray solid that has the lowest density of
any metal. It is an essential component of some advanced
batteries. If a small rectangular slab of lithium weighs 1.49 x 103
mg and has sides that measure 20.9 mm by 11.1 mm by 11.9 mm, what is the
density of lithium?
2) Galena, an ore of lead, has a volume of 4.6 cm3.
If the density of galena is 7.5 g/cm3, what is the mass (in
kg) of that piece of galena?
6. Measuring Temperature
Temperature
- a measure of
how hot or cold a substance is relative to another substance
- determines
whether there can be heat transfer from one object to another and
determines the direction of heat flow
- temperature is
an ________________________property
Three temperature scales in use today:
Temperature Conversions:
Sample Problems::
1) Your normal body temperature is 98.6oF. Convert this
temperature to oC.
2) Many laboratories use 25 oC as a standard
temperature. What is this temperature in oF? in K?
3) Liquefied nitrogen boils at 77 K. What is this
temperature in oC?
7. Measuring Time
8. Qualitative and Quantitative Measurements; Precision and
Accuracy
___________________________________ - descriptive,
nonnumerical form
___________________________________ -
results in a number and unit
_____________________________ - how close a measurement
is to the real value
_____________________________ - how close the
measurements in a series are to each other
To evaluate accuracy:
|